二叉树的先序遍历、中序遍历和后序遍历

一、前言

二叉树是一种非常重要的数据机构，对树节点的访问方式包括了深度优先遍历（DFS）和广度优先遍历（BFS）。其中深度优先遍历包括了先序遍历、中序遍历和后序遍历，广度优先遍历也就是层次遍历。下边只讲深度优先遍历的这三种。

二、三种遍历方式的区别

先上张二叉搜索树（Binary Search Tree）图

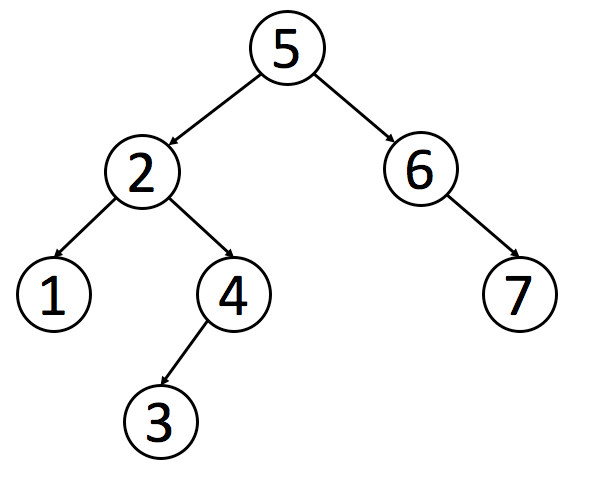
1. 先序遍历

• 遍历方式：根节点 -> 左子树 -> 右子树

• 遍历结果：5214367

2. 中序遍历

• 遍历方式：左子树 -> 根节点 -> 右子树
• 遍历结果：1234567

3. 后序遍历

• 遍历方式：左子树 -> 右子树 -> 根节点
• 遍历结果：1342765

三、Python实现

二叉树的实现代码

class TreeNode(object):
    """
    定义二叉树节点
    """
    def __init__(self, x):
        self.val = x
        self.left = None
        self.right = None

1. 先序遍历

（1） 递归实现

class Solution(object):
    """递归实现二叉树的"""
    def preorder(self, p):
        """
        :type p: 二叉树根节点
        """
        # 保存遍历结果
        result = []
        self.recursion(result, p)
        return result

    def recursion(self, result, root):
        # 节点为None
        if not root:
            return 

        result.append(root.val)
        # 先遍历左子树再遍历右子树
        self.recursion(result, root.left)
        self.recursion(result, root.right)

（2）非递归实现

class Solution(object):
    """非递归实现先序遍历"""
    def preorder(self, p):
        # 保存遍历结果
        result = []
        # 临时保存节点
        stack = []
        while p or stack:
            # 节点非None
            while p:
                result.append(p.val)
                stack.append(p)
                p = p.left
            p = stack.pop()
            p = p.right

        return result

2. 中序遍历

（1）递归实现

class Solution(object):
    def midorder(self, p):
        # 保存遍历结果
        result = []
        self.recursion(result, p)
        return result
    def recursion(self, result, p):
        if not p:
            return 
        self.recursion(result, p.left)
        result.append(p.val)
        self.recursion(result, p.right)

（2）非递归实现

class Solution(object):
    def unrecursion(self, p):
        # 保存遍历结果
        result = []
        # 临时保存节点的栈
        stack = []

        while p or stack:
            while p:
                stack.append(p)
                p = p.left

            p = stack.pop()
            result.append(p.val)
            p = p.right
        return result

3、后序遍历

（1）递归实现

class Solution(object):
    def post_order(self, root):
        result = []
        self.recursion(result, root)
        return result

    def recursion(self, result, root):
        if not root:
            return

        self.recursion(result, root.left)
        self.recursion(result, root.right)
        result.append(root.val)

    def unrecursion(self, root):
        """
        type root: 树根节点
        非递归
        """
        # 保存遍历结果
        result = []
        stack = []

        stack.append(root)
        while stack:
            n = stack.pop()
            if n.left:
                stack.append(n.left)
            if n.right:
                stack.append(n.right)
            # 保存的结果为根右左
            result.append(n.val)
        return result[::-1]

层次遍历

class Solution(object):
    def level(self, root):
        # 保存遍历结果
        result = []
        # 临时保存节点的队列
        queue = []
        queue.append(root)
        while queue:
            root = queue.pop(0)
            if root.left:
                queue.append(root.left)
            if root.right:
                root.append(root.right)
        return result