一、题目描述
给定一组不含重复元素的整数数组 nums,返回该数组所有可能的子集(幂集)。
说明:解集不能包含重复的子集。
示例:
输入:nums = [1, 2, 3]
输出:
[
[3],
[1],
[2],
[1,2,3],
[1,3],
[2,3],
[1,2],
[]
]二、思路 & 代码实现
1. 利用 Python 的 itertools 库的 combinations函数
(1)描述
itertools — 为高效循环而创建迭代器的函数(Python文档中的描述)
本模块实现一系列 iterator ,这些迭代器受到APL,Haskell和SML的启发。为了适用于Python,它们都被重新写过。本模块标准化了一个快速、高效利用内存的核心工具集,这些工具本身或组合都很有用。它们一起形成了“迭代器代数”,这使得在纯Python中有可能创建简洁又高效的专用工具。(Python文档描述)
itertools.combinations(iterable, n)
结果返回由可迭代对象 iterable 中的元素组成的长度为 n 的子序列(每个子序列都是元组的形式;当 n 大于 iterable 序列的长度时,返回的子序列与 iterable 一样)
返回的结果是按照 iterable 的顺序发出的,如果 iterable 有序,则结果按照已排序的顺序发出。
如果 iterable 中有重复的元素,但是不同位置的元素依然会被认为是不同的。
(2)代码实现
from itertools import combinations
class Solution(object):
def subsets(self, nums):
"""
:type nums: List[int]
:rtype: List[List[int]]
"""
# 保存结果
result = []
# 因为iterable的子集也包括它本身,所以要+1
for i in range(length(nums) + 1):
for num in combinations(nums, i):
result.append(list(num))
return result(3)表现
| 运行时间 | 击败 | 内存消耗 | 击败 |
|---|---|---|---|
| 16ms | 88.56% | 12.8MB | 6.60% |
2. 递归(回溯)
(1)描述
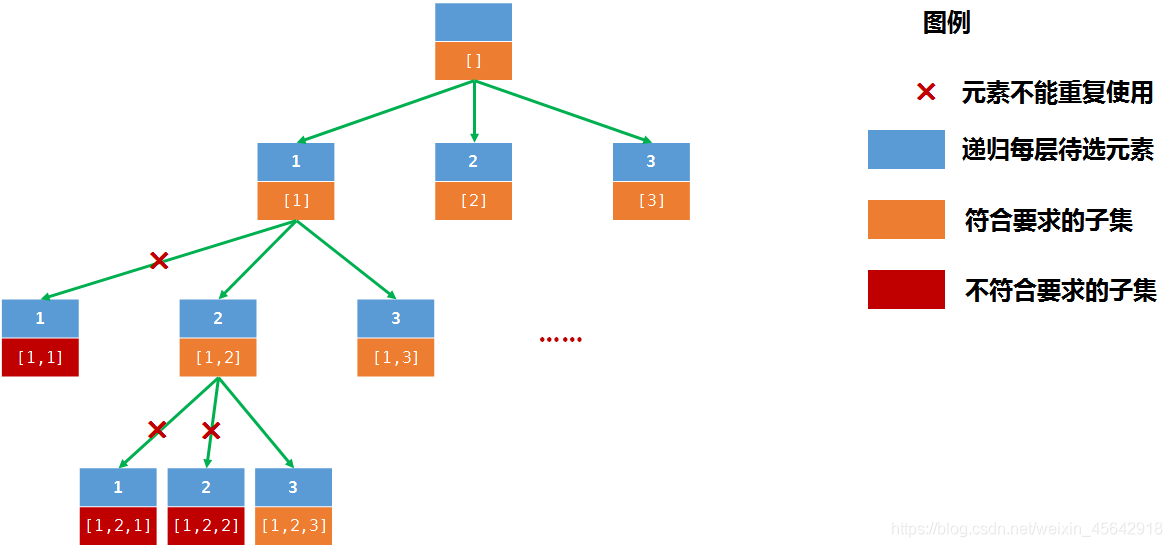
对树结构进行遍历的话,顺序为
[[],[1], [1, 2], [1, 2, 3],[1, 3],[2], [2, 3],[3]]因为解集中包含空集,所以可以在进入递归之前先把子集添加到解集中
元素个数又是有限的,可以不设置递归终止条件
对结果分析,大概的逻辑就是(定义一个数组
ans临时保存子集,数组result保存结果子集):- 进入递归函数内,首先把 ans数组内的 子集保存到数组result中
- 遍历数组nums第一个元素 1,将元素 1 添加到 ans 中,进入递归,以下一个下标为1的元素 2 作为递归起点;进入递归函数首先将 ans 中子集 [1] 添加到 result 中,然后将元素 2 添加到 ans 中,递归。将下一个下标为2的元素 3 的作为递归起点;将 ans 子集 [1,2] 添加到result。将元素 3 添加到ans中 ,将下标3传入进入下一次递归;将子集[1, 2, 3]添加到result中。这时已经不满足遍历条件,此次递归结束,返回元素3的递归中。
- 在元素3的递归这一层接下来回溯,将ans最后一个元素也就是3删除。然后返回元素2的这层递归,此时ans为[1, 2],接下来依然是回溯,删除元素2,。数组nums的遍历继续,接下来轮到元素3,然后将元素3添加到ans,此时ans为[1, 3],然后进入递归。接下来的操作就与前边的基本一致。
- 到了这里,程序的基本架构就已经出来了。下边写代码。
(2)代码实现
class Solution(object):
def subsets(self, nums):
"""
:type nums: List[int]
:rtype: List[List[int]]
"""
# 1、定义解集、子集的数组
result = []
ans = []
length = len(nums)
# 递归函数
def sets(index):
# 将子集保存到解集中
result.append(ans[:])
# 遍历数组nums
for i in range(index, length):
ans.append(nums[i])
# 递归
sets(i + 1)
ans.pop()
sets(0)
return result(3)表现
| 运行时间 | 击败 | 内存消耗 | 击败 |
|---|---|---|---|
| 16ms | 88.48% | 12.6MB | 49.16% |
3. 位运算
(1)描述
直接上图:
| 0/1序列 | 子集 | 0/1序列对应的二进制数 |
|---|---|---|
| 000 | [] | 0 |
| 001 | [3] | 1 |
| 010 | [2] | 2 |
| 011 | [2,3] | 3 |
| 100 | [1] | 4 |
| 101 | [1,3] | 5 |
| 110 | [1,2] | 6 |
| 111 | [1,2,3] | 7 |
0 表示不在当前对应位置的元素不在子集中;1 表示在子集中。
(2)代码实现
class Solution:
def subsets(self, nums: List[int]) -> List[List[int]]:
result = []
length = len(nums)
n = 1 << length
for i in range(n):
res = []
for j in range(length):
if i >> j & 1:
res.append(nums[j])
result.append(res)
return result(3)表现
| 运行时间 | 击败 | 内存消耗 | 击败 |
|---|---|---|---|
| 44ms | 49.72% | 13.2MB | 98.84% |
4. 迭代(在题解中发现的一种方法)
(1)描述
以示例中的[1, 2, 3]为例:
子集结果为:[[], [1], [1, 2], [1, 3], [2], [2, 3], [3], [1, 2, 3]]
分析:(下边分析 = 表示等号,不代表赋值)
- [] + [1] = [1],同理可得[2],[3]
- 如果设子集初始为[[]],然后[] 与 [1] 相加,将结果 [1] 添加到子集数组中得到 [[], [1]]
- 然后用子集 [[], [1]] 中的元素分别与 [2] 相加得到 [2]、[1, 2],然后将结果再添加到子集中,结果为 [[], [1], [2], [1, 2]]。往下 [3] 类推….
- 最后可得出完整的子集数组
(2)代码实现
class Solution(object):
def subsets(self, nums):
"""
:type nums: List[int]
:rtype: List[List[int]]
"""
result = [[]]
for i in nums:
result = result + [[i] + num for num in result]
return result(3)表现
| 运行时间 | 击败 | 内存消耗 | 击败 |
|---|---|---|---|
| 24ms | 39.88% | 12.6MB | 33.01% |

