一、题目
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为“Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为“Finish”)。
问总共有多少条不同的路径?
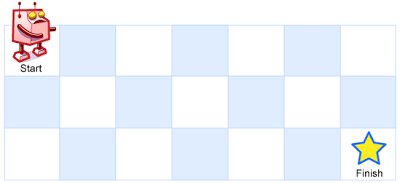
例如,上图是一个 7 x 3 的网格。有多少可能的路径?
示例1:
输入: m = 3, n = 2
输出: 3
解释:
从左上角开始,总共有 3 条路径可以到达右下角。
1. 向右 -> 向右 -> 向下
2. 向右 -> 向下 -> 向右
3. 向下 -> 向右 -> 向右示例2:
输入: m = 7, n = 3
输出: 28提示:
1 <= m,n <= 100- 题目数据保证答案小于等于
2 * 10 ^ 9
二、思路
1. 动态规划
我们可以创建一个二维数组dp,这样一来,在数组中的每一个元素实际上就代表了一个网格。然后我们可以将到达这个网格的所有路径数量保存到对应的数组位置中,数组中所有元素的初始值我们全部设为0。
首先列一张表,表中填充了到达每个位置的路径值,如下所示:
| 1 | 1 | 1 | 1 | 1 |
|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 |
| 1 | 3 | 6 | 10 | 15 |
| 1 | 4 | 10 | 20 | 35 |
| 1 | 5 | 15 | 35 | 60 |
从表中,可以看出,对于nx1、1xm、1x1的情况来说,对应的路径数量全部为1。再往后的每个位置上的值都等于其左侧与上边两个网格值的和。
然后,我们可以创建两个指针i和j,i表示行数,j表示列数。可以得出下列的状态转移方程:
(1)当i == 0 or j == 0,则dp[i][j] = 1
(2)否则呢,则dp[i][j] = dp[i-1][j] + dp[i][j-1]
三、代码
1. 动态规划
class Solution:
def uniquePaths(self, m: int, n: int) -> int:
# n 代表行数,m 代表列数,实际上不影响结果
dp = [[0] * m for _ in range(n)]
for i in range(n):
for j in range(m):
if i == 0 or j == 0:
dp[i][j] = 1
else:
res = dp[i-1][j] + dp[i][j-1]
dp[i][j] = res if res <= 2*(10**9) else 2*(10**9)
return dp[n-1][m-1]四、 表现
| method | 运行时间 | 表现 | 内存消耗 | 表现 |
|---|---|---|---|---|
| 1. 动态规划 | 36ms | 90.79% | 13.6MB | 5.60% |

